排序（Sorting）

• n个记录的序列按照对应的关键字满足的关系，成为一个按关键字有序的序列
• 稳定性：序列R_i领先于R_j，当关键字相等时，排序后的序列中R_i仍领先于R_j，则称排序方法是稳定的；反之，称排序算法是不稳定的
• 快速排序、堆排序和希尔排序等时间性能较好的排序方法是不稳定的

• 排序方法可分为内部排序和外部排序
• 内部排序：指待排序记录存放在计算机随机存储器中进行的排序过程
• 外部排序：指待排序记录的数量很大，以至内存不能一次容纳全部记录，在排序过程中尚需对外存进行访问的排序过程

直接插入排序（Straight Insertion Sort）

• 将一个记录插入到已排好序的有序表中，从而得到一个新的、记录数值1的有序表

• 时间复杂度为O(n²)

• 若带排记录序列为正序时，时间复杂度可提高至O(n)，适合于序列基本有序的情况

• 空间复杂度O(1)

  //从小到大
  void InsertSort(int R[],int n)	//待排序关键字存储在R[]
  {
      int i,j;
      int temp;
      for(i=1;i<n;++i)
      {
          temp=R[i];	//将待插入的关键字暂存于temp中
          j=i-1;
          while(j>=0&&temp<R[j])
          {
              R[j+1]=R[j];	//大于待排关键字，后移一位
              --j;
          }
          R[j+1]=temp;	//找到插入位置
      }
  }

折半插入排序

• 基本思想与直接插入排序类似，区别是查找插入位置的方法不同，折半插入排序采用折半查找法来查找插入位置
• 序列已经有序
• 所需附加空间和直接插入排序相同，时间上比较，折半插入查找仅减少了关键字间的比较次数，记录的移动次数不变，时间复杂度为O(n²)

*2-路插入排序

希尔排序（Shell’s Sort）

• 又称‘’缩小增量排序‘’（Diminishing Increment Sort）
• 基本思想：先将整个带排记录序列分割成若干子序列分别进行直接插入排序，待整个序列中的记录“基本有序”时，再对全体记录进行一次直接插入排序。
• 子序列的构成不是简单地“逐段分割”，而是将相隔某个增量（步长）记录组成一个子序列
• 算法最开始以一定的步长进行排序。然后会继续以一定步长进行排序，最终算法以步长为1进行排序。当步长为1时，算法变为插入排序，这就保证了数据一定会被排序。
• 增量序列中的值应尽量没有除1以外的公因子
• 时间复杂度 ？？？

起泡排序（Bubble Sort）

• 首先将第一个记录的关键字和第二个记录的关键字进行比较，若为逆序，则将两个记录交换，然后比较第二个记录和第三个记录的关键字。依次类推，直至第n-1个记录和第n个记录的关键字进行过比较为止。这称作第一趟起泡排序

• 然后进行第二趟起泡排序，对前n-1个记录进行相同的操作，其结果是使关键字次大的记录被安置到第n-1个位置上，依次类推，直到结束

• 判别起泡排序结束的条件：在一趟起泡排序过程中没有进行交换记录的操作

• 时间复杂度：O(n²)

  void BubbleSort(int R[],int n)
  {
      int i,j,flag;
      int temp;
      for(i=n-1;i>=1;--i)
      {
          flag=0;		//标记本趟排序是否发生交换
          for(j=1;j<=i;++j)
          {
              if(R[j-1]>R[j])
              {
                  temp=R[j];
                  R[j]=R[j-1];
                  R[j-1]=temp;
                  flag=1;
              }
          }
         	if(flag==0)		//说明序列已经有序
          	return;
      }
  }

快速排序（Quick Sort）

• 基本思想：通过一趟排序将待排记录分割成独立的两部分，其中一部分记录的关键字均比另一部分记录的关键字小，则可分别对这两部分记录继续进行排序，以达到整个序列有序

• 任取一个记录作为枢轴（支点），将所有关键字比它小的记录安置在它的位置之前，所有关键字比它大的记录安置到它的位置之后，将序列分割成两个子序列。这个过程称为一趟快速排序。

• 在对分割所得的两个子序列进行快速排序，直至待排序列中只有一个记录。

• 时间复杂度：O(nlogn)；同数量级的排序方法中，其平均性能最好

• 空间复杂度：O(logn)，递归需要栈的辅助

  void QuickSort(int R[],int low,int high)//对从R[low]到R[high]的关键字进行排序
  {
      int temp;
      int i=low,j=high;
      if(low<high)
      {
          temp=R[low];
          while(i<j)	//一趟排序，即将数组中大于temp的关键字放在右边，小于temp的放在左边
          {
              while(j>i&&R[j]>=temp)
                  --j;	//从右往左扫描，找到一个小于temp的关键字
              if(i<j)
              {
                  R[i]=R[j];	//放在temp左边
                  ++i;	//i右移一位
              }
              while(i<j&&R[i]<temp)
                  ++i;	//从左往右扫描，找到一个大于temp的关键字
              if(i<j)
              {
                  R[j]=R[i];	//放在temp右边
                  --j;	//j左移一位
              }
          }
          R[i]=temp;	//将temp放在最终位置
          QuickSort(R,low,i-1);	//递归，对temp左边的关键字进行排序
          QuickSort(R,i+1,high);	//递归，对temp右边的关键字进行排序
      }
  }

简单选择排序（Selection Sort）

• 通过n-i次关键字间的比较，从n-i+1个记录中选出关键字最小的记录，并和第i（1<=i<=n）交换

• 时间复杂度：O(n²)

  void SelectSort(int R[],int n)
  {
      int i,j,k;
      int temp;
      for(i=0;i<n;++i)
      {
          k=i;
          for(j=i+1;j<n;++j)	//从无序序列中找到最小值
              if(R[k]>R[j])
                  k=j;
          temp=R[i];
          R[i]=R[k];
          R[k]=temp;
      }
  }

*树形选择排序（Tree Selection Sort）(锦标赛排序)

堆排序（Heap Sort）

• 将序列看成是一个完全二叉树，则堆的含义表明，完全二叉树中所有非终端结点的值均不大于（或不小于）其左、右孩子结点的值；由此，则堆顶元素（根）必为序列中n个元素的最小值（或最大值）。

• 输出堆顶的最小值之后，使得剩余n-1个元素的序列重建成一个堆；反复执行，得到一个有序序列，这个过程称为堆排序

• 最大堆

  

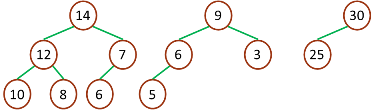
• 最小堆

  

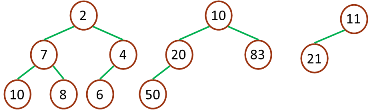
• 创建最大堆（Build-Max-Heap）：将堆所有数据重新排序，使其成为最大堆，由无序列表建成一个堆

• 最大堆调整（Max-Heapify）：将堆的节点作调整，使得子节点永远小于父节点

  

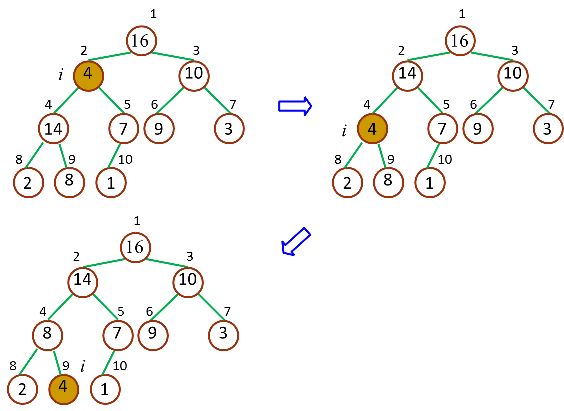
• 堆排序在最坏的情况下，时间复杂度也为O(nlogn)

• 空间复杂度O(1)，仅需一个记录大小供交换用的辅助存储空间

  void Sift(int R[],int low,int high)	//关键字从数组下标1开始
  {
      int i=low,j=2*i;	//R[j]是R[i]的左孩子结点
      int temp=R[i];
      while(j<=high)
      {
          if(j<high&&R[j]<R[j+1])	//若右孩子较大，则把j指向右孩子
              ++j;
          if(temp<R[j])
          {
              R[i]=R[j];	//将R[j]调整到双亲节点的位置
              i=j;	
              j=2*i;
          }
          else
              break;	//调整结束
      }
      R[i]=temp;		//被调整的结点放入最终位置
  }
  
  void heapSort(int R[],int n)
  {
      int i;
      int temp;
      for(i=n/2;i>=1;--i)	//建立初始堆
          Sift(R,i,n);
      for(i=n;i>=2;--i)	//进行n-1次循环，完成堆排序
      {
  		temp=R[1];
           R[1]=R[i];
           R[i]=temp;
           Sift(R,1,i-1);
      }
  }

归并排序（Merging Sort）

• “归并”：将两个或两个以上的有序表组合成一个新的有序表
• 假设初始序列有n个记录，看成是个有序的子序列，每个子序列长度为1，然后两两归并；得到的有序子序列再两两归并，……，直至得到一个长度为n的有序序列为止，这种排序算法称为2-路归并排序
• 多路归并排序
• 时间复杂度：O(nlogn)
• 需要和待排记录等数量的辅助空间

基数排序（Radix Sorting）

• 基本思想：从最低位开始，依次进行一次稳定排序，位数不足的前面补0，直到最高一位也完成一次稳定排序。
• 最高位优先法（MSD法）
• 最低位优先法（LSD法）
• 链式基数排序
• 时间复杂度：O（d*n）